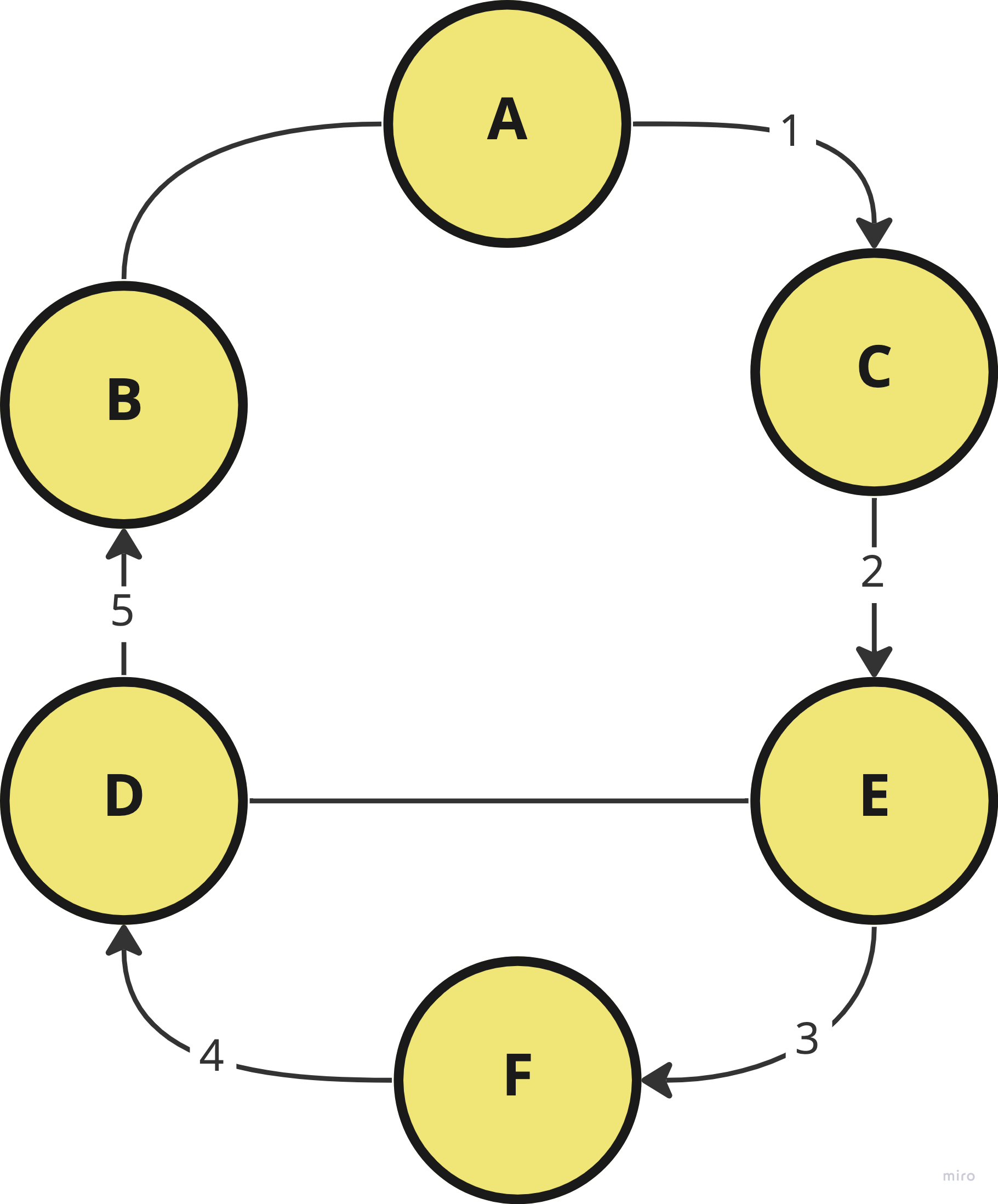
DFS (깊이 우선 그래프 순회)

트리는 그래프의 일종으로, 그래프 자체는 한 노드에서 다른 노드로 갈 수 있는 경로가 트리에 비해 더 많아집니다.

여러 갈래로 연결된 그래프에서 최단 거리를 찾는 것과 같은 작업에서 ‘그래프 순회’의 방법을 사용하게 되며, 예시는 아래와 같습니다.

• 위키피디아의 링크 내 이동 시 최단 거리 찾기
• 페이스북의 친구 추천 시 최단 거리의 다른 친구 추천하기 기능
• GPS 네비게이션
• 미로 문제 풀기

DFS (깊이 우선 그래프 순회)

그래프에서의 형제는 트리와 조금 다른 형태로 이루어지게 되고, 이 형제들은 트리와 달리 반드시 같은 래벨은 아닙니다. 이러한 그래프 순회에서 가지를 따라가는 것이 순회의 가장 기본이 됩니다.

핵심은 각 노드마다 있는 가지 중 방문하지 않은 곳을 방문하는 형식으로 이루어집니다. DFS는 그 방법 중에서도 방문한 노드를 바로 따라 들어가 처리를 하고, 이후 형제 노드를 방문하는 방식으로 이루어집니다.

{
  A: [ 'B', 'C' ],
  B: [ 'A', 'D' ],
  C: [ 'A', 'E' ],
  D: [ 'B', 'E', 'F' ],
  E: [ 'C', 'D', 'F' ],
  F: [ 'D', 'E' ]
}

재귀형 DFS 순회

재귀 함수를 사용하는 방법으로 DFS를 구현하고, 이를 통해 그래프를 순환하게 됩니다. 그래프를 순환하는 함수는 아래 코드와 같습니다.

depthFirstRecursive(vertex) {
  const result = [];
	// 결과를 담을 배열
  const visited = {};
	// 방문한 곳을 나타내는 객체
  const { graph } = this;
	// 해당 함수가 사용되는 전체 그래프
  const dfs = (point) => {
    if (!point) return null;
		// 값이 없을경우에 대한 예외 처리
    visited[point] = true;
		// dfs가 사용되었으므로 방문했음을 표기
    result.push(point);
		// 결과에 해당 포인트에 대한 결과 입력
    graph[point].forEach((nextPoint) => {
		// 해당 포인트와 연결된 다음 포인트에 대해서 처리
      if (!visited[nextPoint]) dfs(nextPoint);
			// 다음 포인트가 방문되지 않았을 경우, 해당 포인트를 방문하여 함수를 처리
    });
  };
  dfs(vertex);
	// 시작 지점에서 처리 시작

  return result;
}

console.log(g.depthFirstRecursive("A"));
// [ 'A', 'B', 'D', 'E', 'C', 'F' ]

재귀형으로 그래프를 탐색하는 경우 크게 ‘방문관련 객체’, ‘결과 배열’, ‘각 포인트의 방문 여부에 따른 재귀 처리’의 세 가지 특징이 있습니다.

여기서는 A라는 포인트로 시작을 했으나, 이는 꼭 A에서만 진행할 필요가 없으며, 어떠한 포인트에서 돌든 결국 모든 포인트를 거쳤다는 사실이 중요합니다.

반복형 DFS 순회

while을 이용한 반복문 처리를 통해 DFS 순회를 하게 됩니다.

depthFirstIterative(vertex) {
  const result = [];
  // 결과 배열
  const visited = {};
  // 방문 확인 배열
  const { graph } = this;
  // 현재 그래프
  const stack = [vertex];
  // 처리해야할 stack 배열. 처음에는 설정된 값 하나만 들어옴

  let curVertex;
  visited[vertex] = true;
  // while문을 돌면서 현재의 위치를 나타내는 변수
  while (stack.length) {
    curVertex = stack.pop();
    // DFS를 실행하기 위해, 뒤에 있는 값부터 처리하는 것이 중요!
    result.push(curVertex);
    // 결과에 방문에 대한 결과값 처리
    graph[curVertex].forEach((nextVertex) => {
      // 현재 위치의 다음 위치들에 대해서 방문 여부 확인
      if (visited[nextVertex]) return;
      // 방문하지 않았을 시 stack에 추가
      visited[nextVertex] = true;
      // 방문을 했으므로 true처리 => stack에 들어오는 것으로 실질적인 계산을 하기 때문에,
      // stack에 넣기 바로 전에 처리를 해주어야 에러가 발생하지 않음
      stack.push(nextVertex);
    });
  }

  return result;
}

반복을 사용하는 경우 while문을 쓰게 됩니다. 그리고 ‘결과’, ‘방문’, ‘처리할 값들’을 나타내는 배열이나 객체가 필요합니다.

while을 돌면서 처리를 하게 되는데, 이 때 현재 위치에 대해서 필요한 처리(여기서는 결과 배열에 추가)를 하게 되며, 이후 다음 위치들에 대해서 방문 여부를 확인 후 stack에 넣어주는 방식으로 진행합니다.

그래프의 형태가 같아도, 다른 결과가 나올 수 있게 되는데, 이는 배열에 주입된 순서에 따라 B와 C 중 어느 것이든 먼저 갈 수 있고, 이에 따라 깊이 우선의 순서가 바뀌기 때문입니다. 하지만, 모든 곳을 깊이 우선으로 탐색한다는 데에는 변함이 없습니다.

GITHUB  EMAIL