BINARY HEAP ∙ PRIORITY QUEUE
ALGORITHM ·해당 내용은 UDEMY의 알고리즘 ∙ 자료구조 강의를 수강 후 정리한 내용입니다.
이진 힙(Binary Heap)
두 개의 자식 노드를 가지며 부모 노드가 무조건 자식 노드보다 크거나(최대 이진 힙) 작은(최소 이진 힙) 구조를 의미합니다. 이진 검색 트리와 매우 비슷하나 몇 가지 다른 규칙들이 존재하는데, 최대 이진 힙의 경우, 부모 노드가 자식 노드보다 항상 큰 값을 가지고 최소 이진 힙에서는 이와 반대되어 존재합니다. 또한, 이진 힙은 언제나 최적의 용량을 가져, 가장 적은 용량을 채웁니다.
힙을 통해서 ‘우선순위 큐’라는 것을 만들 수 있으며(항상 이진 힙이 사용), 그래프 순회에도 자주 사용됩니다.
힙 정렬
앞서 말했듯, 힙 정렬은 이진 검색 트리와 다른 점으로 크기의 순서가 정해졌다는 것(큰 순서 ∙ 작은 순서)과 왼쪽이 무조건 먼저 들어온다는 것이 있습니다.
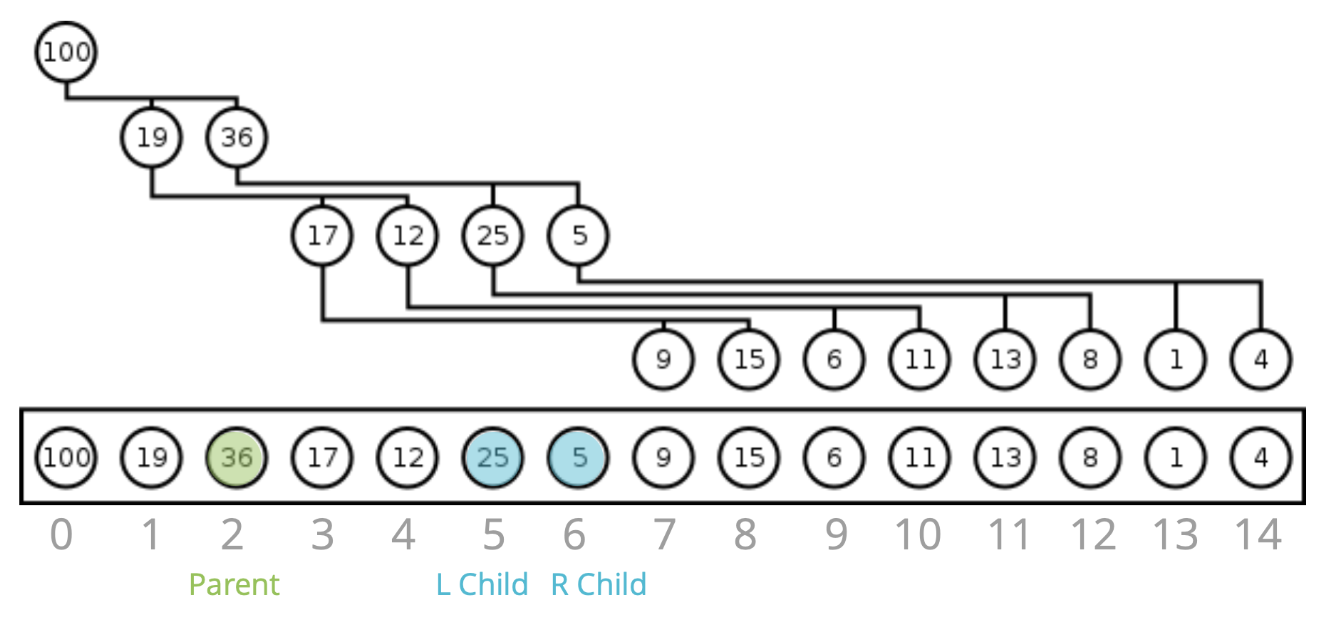
위 그림으로 보면 index가 n인 값의 왼쪽 자식은 2n+1, 오른쪽 자식은 2n+2의 인덱스에 저장된 것을 볼 수 있으며, 이를 통해서 부모의 위치를 기반으로 자식의 위치를 찾는 것을 할 수가 있습니다. 예를 들어, index 11, 12의 경우, 각각 1을 빼고 2로 나눌 시 5, 5.5가 되는데 이를 Math.floor()로 표현할 시 5가 되고 이 값은 부모 요소의 index값이 됩니다.
Insert 메소드 만들기
기본적으로 만들어지는 Binary Heap 클래스의 constructor는 values=[] 밖에 없으며, 나머지는 메소드를 통해서 이루어집니다.
이진 힙(최대값)을 만드는 과정에서, 이전 값보다 큰 값이 들어올 경우, bubble up을 해야 합니다.
- 부모와 자식 간의 값을 비교해서 자식이 더 큰 경우, 이 둘 사이의 index값을 바꿔줍니다.
- 같은 형식을 반복해서 부모보다 올라가는 값이 작은 경우, 해당 형식을 중단합니다.
class MaxBinaryHeap {
constructor() {
this.values = [41, 39, 33, 18, 27, 12, 55];
// 기본적으로 예시를 들어줄 값을 넣음
}
insert(element) {
this.values.push(element);
this.bubbleUp();
}
bubbleUp() {
let index = this.values.length - 1;
// push되어 들어간 값이 마지막에 위치하므로 index를 위와 같이 설정
const element = this.values[index];
// 현재 push되어 들어온 값
while (index > 0) {
// index가 현재 최대 이진 힙의 첫 자리보다 큰 경우 중단
let parentIndex = Math.floor((index - 1) / 2);
// 앞에서 나온 바와 같이, 현재 index의 부모 index는 1을 빼고 2로 나눈 값의 내림과 같음
let parent = this.values[parentIndex];
// 부모 값을 구하고 비교
if (parent >= element) break;
// 부모 값이 더 작을 경우, 서로 위치를 바꿔주고 index값을 부모 값으로 만듬
this.values[parentIndex] = element;
this.values[index] = parent;
index = parentIndex;
}
}
}
const heap = new MaxBinaryHeap();
heap.insert();
extractMax 메소드 만들기
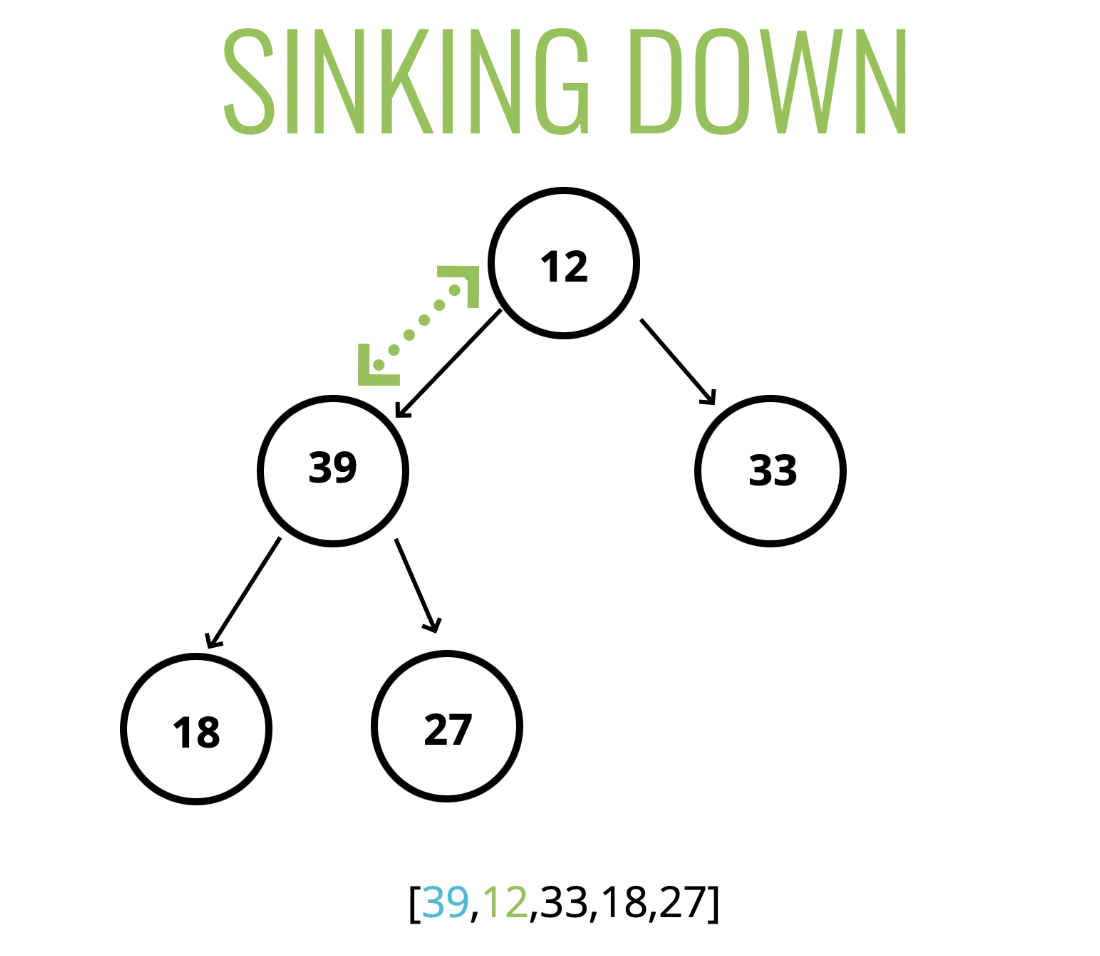
최대 이진 힙에서는 루트가 가장 큰 값을 갖게 되고, 이 값을 제거해주면 됩니다. 그리고 이 때 제거되고 비어있는 값을 그대로 내버려 둘 수는 없기 때문에, 이 부분을 가장 하단의 것과 교체하고 이를 내리는 작업이 필요합니다.이 과정을 버블 다운, 퍼콜레이트 다운, 시프트 다운, 싱크 다운 등의 단어들로 불립니다. 순서는 아래와 같습니다.
- 최대 값을 빼내고 해당 위치에 가장 마지막 인덱스의 값을 넣기
- 루트에 위치한 값의 좌측 → 우측 순서로 보면서 루트값보다 큰 값이 있을 시 그 값과 교체
- 교체하는 작업을 지속한 뒤, 좌측에 값이 없거나 양측의 값이 현재 값보다 작은 경우 교체 작업 중단
- 좌 ∙ 우의 값 중 더 큰 값과 교체를 해야하므로, 좌측의 값 확인 후 우측의 값을 확인해 교체
extractMax() {
const max = this.values[0];
// 최대 값을 먼저 저장함
const lastValue = this.values.pop();
// 마지막 값을 빼내어 갖고 있음
if (this.values.length) {
// 해당 정렬의 개수가 1개일 경우, pop을 하고 난 뒤에 다시 sinkDown으로 넣어주는 것을 방지
this.values[0] = lastValue;
this.sinkDown();
}
return max;
// 최대값을 리턴함
}
sinkDown() {
const { length } = this.values;
const element = this.values[0];
// 계속 움직이면서 넣어주게 될 값
let index = 0;
// 처음에는 index가 루트에서 출발하므로 0에서 시작
while (true) {
const leftIndex = index * 2 + 1;
const rightIndex = index * 2 + 2;
let swap = null;
// 현재 index와 바뀌게 될 index를 swap으로 설정
let leftChild, rightChild;
if (leftIndex < length) {
// 왼쪽 인덱스 값이 존재하고 해당 값이 기존 값보다 클 경우 swap에 저장
leftChild = this.values[leftIndex];
if (leftChild > element) {
swap = leftIndex;
}
}
if (rightIndex < length) {
// 좌측보다 우측 값이 더 크고, 해당 값보다도 더 클 때 swap에 저장
rightChild = this.values[rightIndex];
if (
(!swap && rightChild > element) ||
(swap && rightChild > leftChild)
) {
swap = rightIndex;
}
}
if (!swap) break;
// swap에 없을 시 왼쪽 오른쪽 값보다 해당 값이 더 크다고 판단
this.values[index] = this.values[swap];
this.values[swap] = element;
// swap에 들어온 값과 서로 바꿔줌
index = swap;
// 새로운 index로 바꾼 위치를 설정
}
}
우선 순위 큐(Queue)
각 요소가 그에 해당하는 우선순위를 가지는 데이터 구조입니다. 서로 다른 우선순위를 가지는 데이터나 정보를 관리할 필요가 있는 상황에서 활용할 수 있으며, 먼저 들어간 값이 존재한 상황에서도 이후에 들어온 값이 우선 순위를 갖고 있으면, 해당 값이 먼저 처리가 될 수 있도록 할 수 있습니다.
예시로 ‘유닉스’가 있는데, 여기서 프로세서 ID라고 할 수 있는 ‘나이스’가 우선순위의 역할을 합니다. 대부분은 입력된 순서대로 처리가 되지만, 간혹 다른 것들이 앞서서 실행되는 상황이 발생하기도 하며 이러한 상황에서 사용한다고 볼 수 있습니다.
우선 순위 큐와 힙은 별개의 것으로 생각해야 하는데, 이는 그저 추상적인 개념에 불과하기 때문입니다.

예시로 위 사진을 보면, 우선순위가 가장 높은 1번을 찾아야하는데, 이 상황에서 별 다른 방법없이 직접 비교해가며 찾는 것을 할 경우, 1을 발견하고 나서 다른 것들이 1번보다 앞서는 지를 지속적으로 확인해야 한다는 문제점이 발생하게 됩니다. 이러한 상황에 우선 순위 큐를 활용할 수 있습니다.
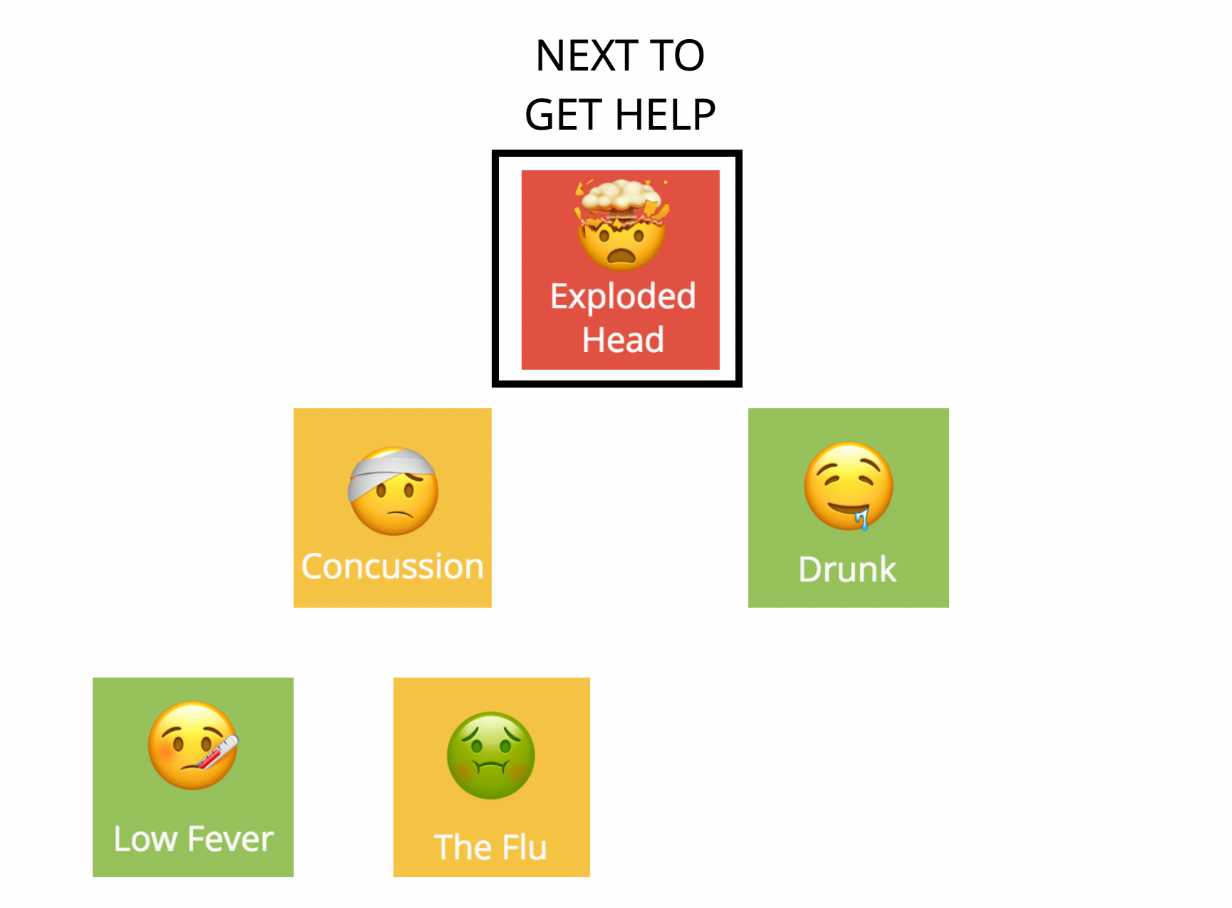
위 예시 사진과 같이 우선 순위를 지정할 때, 이전에 있었던 요소들보다 더 우선순위가 높은 것이 들어오게 되면 이를 bubble up 시켜서 순위를 높이는 방식으로 문제를 처리할 수 있습니다. 이러한 방식의 처리는 O(logN)의 시간 복잡도가 나오고, 앞선 예시의 처리방식(시간복잡도가 O(N))보다 훨씬 효율적으로 처리를 할 수 있습니다.
우선 순위 큐 코드 작성
class PriorityQueue {
constructor() {
this.values = [];
}
enqueue(value, priority) {
const newNode = new Node(value, priority);
this.values.push(newNode);
this.bubbleUp();
}
bubbleUp() {
let index = this.values.length - 1;
const element = this.values[index];
while (index > 0) {
let parentIndex = Math.floor((index - 1) / 2);
let parent = this.values[parentIndex];
if (parent.priority >= element.priority) break;
this.values[parentIndex] = element;
this.values[index] = parent;
index = parentIndex;
}
}
dequeue() {
const max = this.values[0];
const lastValue = this.values.pop();
if (this.values.length) {
this.values[0] = lastValue;
this.sinkDown();
}
return max;
}
sinkDown() {
const { length } = this.values;
const element = this.values[0];
let index = 0;
while (true) {
const leftIndex = index * 2 + 1;
const rightIndex = index * 2 + 2;
let swap = null;
let leftChild, rightChild;
if (leftIndex < length) {
leftChild = this.values[leftIndex];
if (leftChild.priority > element.priority) {
swap = leftIndex;
}
}
if (rightIndex < length) {
rightChild = this.values[rightIndex];
if (
(!swap && rightChild.priority > element.priority) ||
(swap && rightChild.priority > leftChild.priority)
) {
swap = rightIndex;
}
}
if (!swap) break;
this.values[index] = this.values[swap];
this.values[swap] = element;
index = swap;
}
}
}
class Node {
constructor(value, priority) {
this.value = value;
this.priority = priority;
}
}
const queue = new PriorityQueue();
queue.enqueue("A", 1);
queue.enqueue("B", 5);
queue.enqueue("C", 2);
console.log(queue.values);
console.log(queue.dequeue());
위 코드를 보면, 이진 힙을 만들 때 사용했던 코드를 그대로 활용해서 만들 수 있습니다. 이 중에 달라진 것은 Node라는 클래스가 추가되고, 내부에 value(자체적인 값), priority(우선 순위)가 추가된다는 것입니다.
비교를 할 때 이진 힙에서는 값 자체로 비교를 했으나, 여기서는 추가적인 Node 클래스를 만들었기 때문에 내부에 있는 priority로 비교를 해주면 됩니다. 현재 위 코드는 최대 이진 힙으로 만들어진 것을 변형했지만, 여기서 부등호만 변경해주면 최소 이진 힙으로 만들 수 있으며, 이를 통해 priority가 작은 값이 가장 위에 위치하도록 설정할 수 있습니다.
현재 코드는 우선 순위로만 비교를 하지만, 실제 활용 시에는 우선 순위외에 다른 요소들이 들어올 수 있어, Node 클래스에 해당 요소를 추가하고 이를 enqueue나 dequeue에서 더 활용하면서 우선 순위를 지정해줄 수 있습니다.
우선 순위 큐는 위와 같은 과정을 통해서 삽입과 제거 모두 O(logN)의 시간 복잡도를 가집니다.
이진 힙의 BIG O
이진 힙의 경우 O(logN)의 시간 복잡도를 가지는데, 이는 상당히 빠른 속도로 문제를 해결할 수 있다는 것을 알 수 있습니다. (logN이라는 것은 2를 밑으로 하는 log의 N배라는 것을 의미)
예를 들어, 노드가 5개의 층인 경우, 총 2의 5제곱의 노드들이 생성되게 되는데, 이러한 상황에서도 노드가 추가될 때에는 총 5의 시간 복잡도를 갖게 됩니다.

최악의 상황이 위 사진과 같이 나올 수 있는데, 이런 경우에는 heap을 사용할 수가 없습니다. 왜냐하면 heap은 기본적으로 이러한 모양이 될 수가 없다는 것을 전제(무조건 왼쪽 ∙ 오른쪽 순서로 값을 채워나감)로 하기 때문
이진 힙에서 값을 찾아야 하는 경우에는 O(N)의 시간복잡도가 나오게 됩니다. 즉, 이진 힙은 탐색보다는 삽입과 제거를 다루는 상황에 가장 최적화된 구조라는 것을 알 수 있습니다.