백준 22871번

QUESTION LINK

‘다이나믹 프로그래밍’으로 풀어야하는 문제였습니다. 해당 문제의 경우, 한 칸씩 이동을 할 때마다 해당 칸까지 갔던 거리의 최소값들을 구해주는 식으로 진행을 해야 문제를 풀 수 있었습니다. 그림으로 보면 아래와 같습니다.

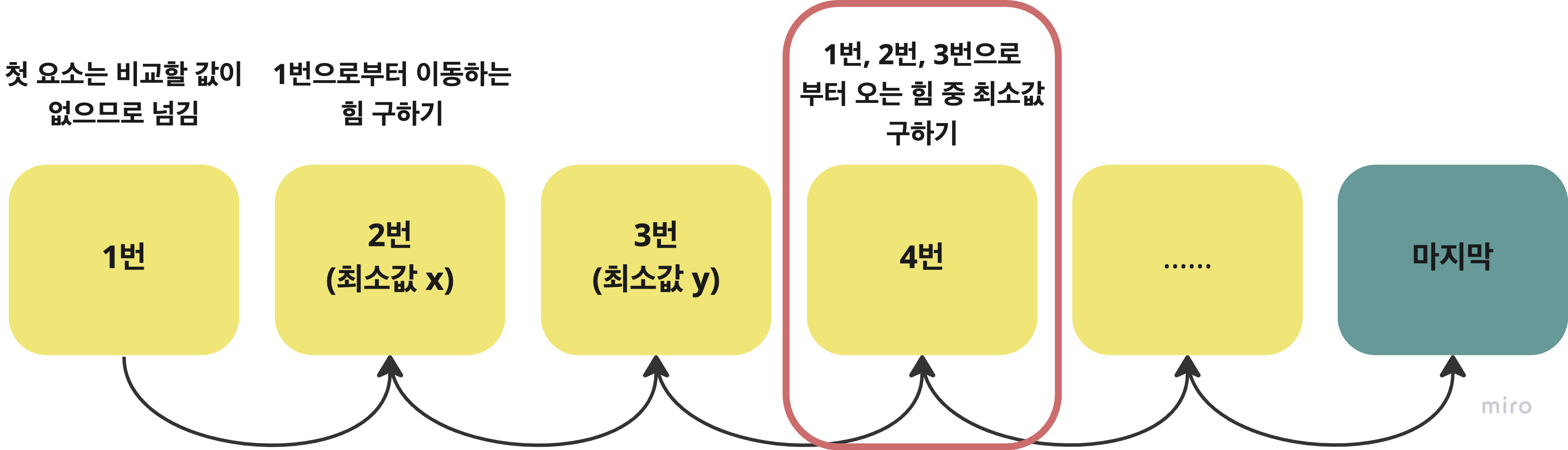
위 그림을 통해서 보면, 2번과 3번을 지나면서도 각각에 대한 최소값들을 만들고 넘어오는 것을 볼 수 있습니다. 여기서 4번을 예시로 들면 4번에 오는 최단거리의 값을 만들 때에는 ‘1번 → 2번 → 4번’, ‘1번 → 3번 → 4번’으로 오는 방법이 존재하게 되는데, 여기서 2번을 지나갈 때와 3번을 지나갈 때 각각 미리 그 곳을 종점으로 하는 최소값을 기록한 다음에 넘어오면, 4번에서도 같은 방식으로 4번까지 오는 최소값을 구할 수 있게 되는 것입니다.

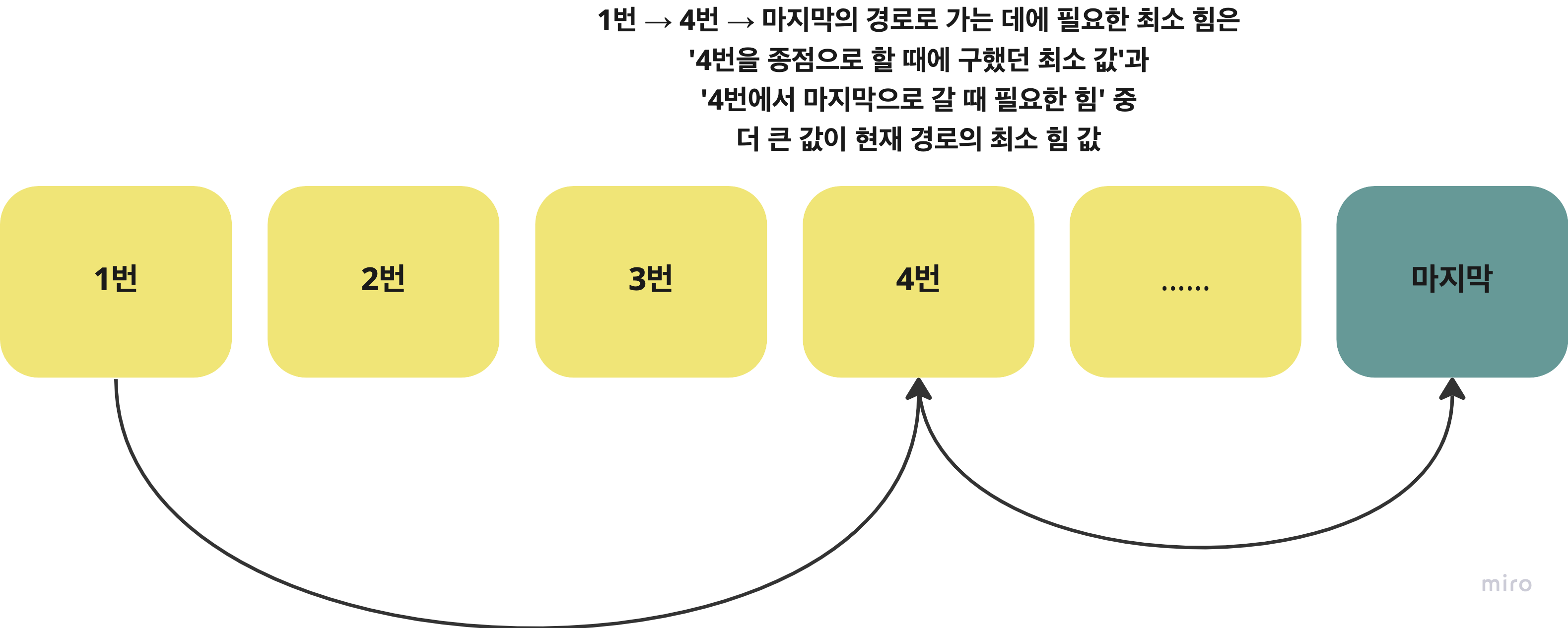
즉, 주어진 값들에 대한 배열을 돌면서 각 index까지 도달하기 위한 최소값들을 구하고 이를 일종의 배열에 담고 있으면, 그 배열의 마지막 값이 곧 ‘종점으로 가기 위해 최소로 요구되는 힘’이 됩니다. 코드로 나타내면 아래와 같습니다.

const [_, valuesString] = fs
  .readFileSync(filePath)
  .toString()
  .trim()
  .split("\n");
const values = valuesString.split(" ").map(Number);
// 들어온 값들을 숫자로 정리한 배열
const distances = [];
// 각 인덱스까지 오는 데에 필요한 최소 힘을 담는 배열

values.forEach((value, index) => {
  // 배열의 각 index들을 돌면서 해당 index까지 도달하기 위한 최소 힘을 구함
  if (!index) return;
  // index가 0인 경우에는 혼자 있으므로 관련없음

  for (let i = 0; i < index; i += 1) {
    // 출발지를 0부터 index - 1까지로 하여, 0, i, index의 경로로 오기 위한 최소힘을 구함
    const curPower = (index - i) * (1 + Math.abs(value - values[i]));
    // 순회하는 배열에서의 종점과 for문을 통해 돌고 있는 i 사이의 필요힘
    const power = distances[i] ? Math.max(curPower, distances[i]) : curPower;
    // i까지 오는 데에 대한 최소값이 없을 시는 현재 구한 값이 최소 힘이며,
    // 아닐 시 이미 구한 최소 힘과 비교하여 더 큰 값을 현재 필요힘으로 설정
    distances[index] = distances[index]
      ? Math.min(power, distances[index])
      : power;
    // 이전에 설정된 index의 최소 힘과 비교하여 더 작은 값이 있을 시
    // 그 값이 index에 도달하기 위한 최소 힘 값이 됨
  }
});
console.log(distances[distances.length - 1]);

문제 자체에 대한 이해는 어렵지 않았으나, 이를 구현하는 과정을 생각하는 데에 시간이 오래 걸렸습니다. 무엇보다, distances라는 배열을 구상하고 이 배열을 통해서 지속적으로 값을 비교해나가며 최소값을 찾아가는 과정이 어려웠습니다. 이와 같은 문제를 마주쳤을 때, 이 코드의 distances와 같은 형태의 배열을 만들고, 비교해가는 과정이 이루어져야함을 알 수 있었습니다.

GITHUB  EMAIL