디지털 논리회로

디지털 논리회로란?

이산적인 숫자를 게이트 입력으로 받아, 입력 논리의 필요 조건을 만족, 불만족하는 지에 대해 1 또는 0의 신호로 출력하는 하드웨어 소자이다.

디지털 논리회로의 연결을 통해 컴퓨터의 구성 부품을 만들게 된다.
또한, 논리적 사고를 위한 가장 기본적인 동작으로 프로그래밍 논리 구조와 연결된다.

종류

• AND 게이트(논리곱) : 두 입력 모두 1인 경우에만 1, 나머지는 0이 출력된다.

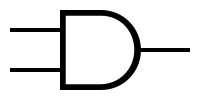
• OR 게이트(논리합) : 두 입력 중 1이 존재할 경우 1, 아닐 시 0이 출력된다.

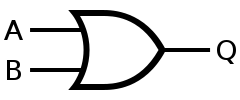
• NOT 게이트(논리부정, INVERTOR) : 입력이 반전되어 출력된다.

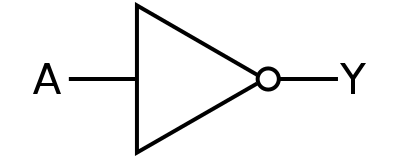
• NAND 게이트 : 두 입력 중 하나 이상 0인 경우 1, 나머지는 0이 출력된다. 즉, 두 입력이 모두 1인 경우 0이 출력된다. AND 게이트와 반대의 역할을 한다.

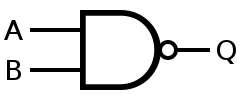
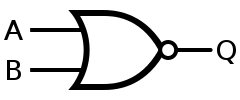
• NOR 게이트(부정논리합) : 두 입력 중 하나 이상 1인 경우 0, 나머지는 1이 출력된다. 즉, 두 입력 모두 0인 경우에 1이 출력된다. OR 게이트와 반대의 역할을 한다.

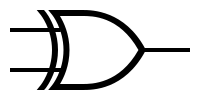
• XOR 게이트(배타적 논리합) : 입력이 같을 경우 0, 다를 경우 1이 출력된다. 참 입력의 개수가 홀수일 때 참을 내보낸다.

이진수

전원이 켜진 상태와 꺼진 상태를 각각 true, false의 형태로 나타낼 수 있으며, 이런 방식을 수학자 조지 부울의 이름을 따서 Boolean 타입이라고 부른다.
Boolean 타입은 논리대수의 기본 타입이며 동시에 디지털 시스템을 구성하는 하드웨어 및 소프트웨어의 가장 기본적인 타입이다.
모든 전자부품은 전기의 흐름 유무로 Boolean 타입을 나타낼 수 있으며, 이 개념의 확장으로 모든 10진수 숫자를 2진수 코드로 나타낼 수 있다.
예시로, 1비트(bit)는 2개(0-1)의 값을 나타낼 수 있고, 2비트는 4개(0-3), 3비트는 8개(0-7)의 값을 나타낼 수 있다. 그리고 이는 각각 2^(비트수)의 형태로 나타난다.

반가산기(half-adder)

두 개의 비트를 더하는 과정에서, 결과값을 2비트의 값으로 표현해볼 수 있다.

+	0	1
0	00	01
1	01	10

왼쪽과 같이 2비트의 값으로 나타낼 수 있고, 한 비트 내의 두 이진수를 더하면, 두 비트가 되어 각각의 비트를 합(sum)비트, 자리올림(carry)비트라고 한다.

• 합비트

	0	1
0	0	1
1	1	0

• 자리올림비트

	0	1
0	0	0
1	0	1

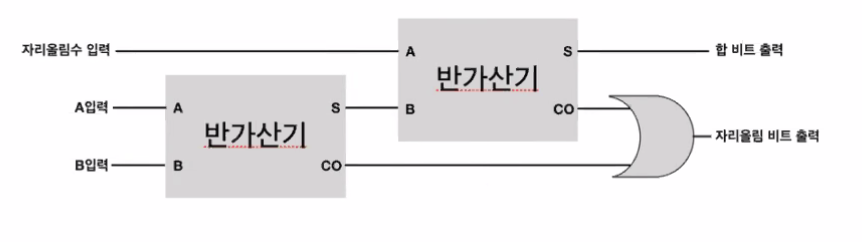
전가산기(full-adder)

두번째 자리부터는 자리올림이 발생한 경우에 대해서도 더해줘야 하기 때문에, 세 개의 이진수를 더하는 경우에는 두 개의 반가산기 및 OR 게이트를 활용하는 전가산기를 사용한다.

---

10진법과 2진법

10진법

10의 배수의 단위로 숫자를 나누어 나타내는 방법이다. 10단위가 올라갈 때마다 숫자가 증가하는 모습을 보인다.

2진법

2의 배수의 단위로 숫자를 나누어 나타낸다. 2단위가 증가 시 숫자가 올라가게 된다. 가장 작은 단위는 2^0 단위로, 이 한 단위를 비트(bit)로 표현하게 된다.

GITHUB  EMAIL